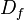Funciones continuas y discontinuas

Las  funciones  continuas   son aquellas cuyas gráficas  se pueden trazara  sin despegar el lápiz de la hoja de papel, mientras que las discontinuas  por lo contrario  presentan interrupciones, huecos o saltos, estas pueden ser en puntos o en ciertos  intervalos.

Por ejemplo, la función polinominal   f ( x ) = X^{3 +} 5  X^{2 +} 1,  es una función  continua  ya que no presenta interrupciones.

Sin embargo las siguientes funciones son descontinuas

En  la gráfica  se observa que la figura  presenta discontinuidad en los puntos de x=2  que hacen cero al denominador; es decir, donde la función no está definida en este caso cuando x= -2 y x= 2

En este caso, para encontrar la ordenada que corresponda a los puntos de discontinuidad, se utiliza una ecuación equivalente a la original, que sea continua en esos puntos y se obtiene  utilizando  un artificio algebraico de la siguientes forma:

Primero: Igualamos el denominador a cero y resolvemos

                X^{2 –} 4= 0

              (x+2) ( x-2)=0

aplicando la propiedad del producto cero tenemos:

                                               x+2=0

                                               x= -2

                                               x-2=0

                                               x= 2

Encontramos que la función se vuelve indeterminada para los valores de

                               X= -2 y x=2

 Segundo:  se factoriza  el numerador y/o el denominador según la función, y se simplifica como se aprecia

A continuación:

                                   h(x)= x⁴-16/x²-4

                                         = (x²+4) (x² - 4)/ (x²  - 4)

                                         = x² +4

 Tercero :  substituimos en la expresión resultante los valores de x= -2y x= 2 para obtener  las ordenadas de los puntos de discontinuidad

 f (-2)= (- 2 )²  + 4= 8

 f( 2) = ( 2) ² + 4= 8

Los puntos de discontinuidad  son: P₁ (-2, 8) y P₂ (2, 8)

 Por lo tanto, el dominio: x€( -∞, -2) U (-2, 2) u ( 2 + 8)

El Rango: y €[ 4, 8 ) U ( 8,+∞)

Otra forma de visualizar lo anterior sería tabulando,

a)      La función siguiente también corresponde a una gráfica discontinua. Dicha discontinuidad  se presenta en los puntos por donde se encuentran Las  asíntotas verticales, en x= -1 y x= O

Clasificaciones con funciones

Podemos clasificar las funciones de acuerdo a la forma de la ecuación que la representa, por su gráfica y por su dominio y rango. A continuación  mostramos un esquema de esta función:

Las  funciones polimiales son aquellas que tienen la forma:

f(x)=a_nxⁿ + a₁xⁿ⁺¹ – a₂xⁿ⁺²-a₃x^n-3 + ………….. + a₀

Ejemplos: f(x)= 6x⁵ +x⁴+3x²- 2x+5

                   F(x)=2x-1

                   F(x)= 3x²-5x+1

Entre las funciones polinomiales también se encuentran la : potencial, la identidad y la constante.

Ejemplos:  

F(x)= x⁴

F(x)= x

F(x)=8

Las funciones algebraicas racionales son aquellas que se expresan como el cociente de dos polinomios, son de la forma, f(x)= p(x)/ q(x) por ejemplo: f(x)= x⁴+2x²-1/ x³+ 2x -3

Las funciones irracionales son aquellas cuyos exponentes son fracciones, son de la forma:

f(x)= x^m/n = ⁿ√x^m

Por ejemplo: f(x)= x^2/3 = ³√x²  

Las funciones transcendentes trigonométricas son: seno, coseno, tangente, cotangente, secante y cosecante.

Ejemplos : f(x)= 2sen(3x)

                  f(x)=-cos(4t)

                  f(x)= tanβ

Las trigonométricas inversas o circulares inversas son: arco seno, arco coseno,…..

Ejemplos: f(x)= arc sen(x)

                 f(x)= arc tan(x)

Las funciones exponenciales son de la forma f(x)= A(b)^x

Ejemplos: f(x)= 2(3)^x

Las logarítmicas son aquellas que presentan la forma f(x)= Alog_bx

Ejemplos: f(x)= 3log₂x

                 f(x)= In(4x)

Operaciones con Funciones

Al  igual que las operaciones con número, las funciones se pueden sumar, restar, multiplicar y dividir.

                Suma:  f( x) ­+ g( x)= ( f+g) (x)

                Resta:  f(x)-g(x) /= ( f-g)( x)

                Multiplicación: f( x). g(x)= (f.g) (x)

                Division:  f(x) /  g(x) = (  f /g) ( x)

El  dominio de la nueva función resultante, es el conjunto de valores para los cuales está definida la función.

Recordemos que en el caso de la división, el domicilio excluyente  el valor o valores de x para los cuales el denominador es cero; es decir, el punto o los puntos para los cuales no está definida la función.

 Por ejemplo:

Si f(x)  = 4x y g(x) =X²-4x+3, efectuamos las operaciones:

a).-  F(x)+ g(x)= (f+g) (x) = 4x + (x²-4x+3)

                                                      = x² + 3

           

             Dominio: x€(-∞, +∞) ó x€R

            b).- F(x)-  g(x)= (f-g) (x) = 4x - (x²-4x+3)

                                                    = 4x-x² + 4x- 3

                                                    =- x² + 8x- 3

                      

             Dominio: x€R 

             c). F(x). g(x)= (f . g) (x) = 4x (x²-4x+3)

                                                    = 4x³-16x² + 12x

                                                         

             Dominio: x€R

             d).-  F(x) / g(x)= (f /g) (x) = 4x /   X² -4x+ 3  =  4x /(x-3)(x-1)  

                                                                                         

             Dominio: x€R

La función no está definida para valores de x=1 y x=3,  puesto que con esos valores el denominador es cero

Por lo tanto, el dominio: x€(-∞, 1) u (1,3) U (3, +∞), también  se puede representar como  {X€Rlx≠1,3}, significando  lo mismo que  -∞< x < 1  U  1 <  x < 3 U 3 < x < + ∞

Existe otra operación que sirve para hacer un cambio de variable,  que se llama composición de funciones  o composición funcional, Esta se puede representar  de la siguiente manera:

( f ⁰ g)  ( x) = f( g ( x), que se lee  “f compuesta con g”.

Por ejemplo, xi f( x)= x²  +2 y g(x)=<-3x+5

Para  encontrar  f(g(x), reemplazamos  x de la función g( x) la expresión f( x), por lo tanto,

 ( f . g)   ( x) = f( g(x) ) = f(-3x+5)

                                     =(-3x+5)  ² + 2

                                      = 9x²-30x+25+2

                                      = 9x²-30x+27

Dominio: x€ R.

Problema resuelto:

 En una tienda de roma, se ofrece una camisa con descuento del 20% sobre el precio de lista  x. El impuesto a pagar por una prenda es de 16%. Si llamamos P(x) al importe a pagar con descuento eI(x) al impuesto a pagar.

           Encuentra :

a)     I(X) ⁰ P( X)

b)     P( X) + I ( X) ⁰ P (X)

 Solución

a)    Si lo que hay que pagar con descuento por x  camisas compradas es P (x)=x-0.2x y lo que hay que para de impuesto  es I (x)=0-16x.

Por  lo tanto,

                                                           I(x) o P ( x) =I ( P( x) )

                                                                              = I ( x-0.2x)

                                                                              = 0.16 ( x-0.2x)

                                                                              =0.16x(1-0.2)

                                                                              =.16x(0.8)

Lo cual indica el impuesto a pagar sobre el precio del artículo después de haberse aplicado el descuento del 16%.

a)   P(x)+I (x)o P(x)=x-0.2x+ 0.16x ( 0.8)

                         = x-0.2x+ 0.128x

                         = 0.928x

       Ésta  expresión nos da a conocer el pago final.

Formas de representar el dominio y rango en una funcion

En una función el dominio y rango son por lo general intervalos cuando no son todo el conjunto de los números reales
En la funcion f (x) = -x

El dominio esta conformado por los numeros que pertencen al conjunto de los reales

Formas de representar rango en una funcion

En una funcion el dominio y el rango son por lo general intervalos cuando no son todo el conjunto de numero s reales.
Por ejemplo
En la funcion f (x) = -x² 




El dominio esta conformado por los números que pertenecen al conjunto de los reales

X€ ( -∞ +∞) ó X € R y el rango por los números del intervalo y Y€ ( -∞ ,0 } ó y <0

Dominio:

 el dominio (conjunto de definición o conjunto de partida) de una función  es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota  o bien . En  se denomina dominio a unconjunto conexo, abierto y cuyo interior no sea vacío.

Contradominio

 el codominio o contradominio denominado conjunto final, recorrido o conjunto de llegada de una función.

Imagen:

La imagen (conocida también como campo de valores o rango) de una función  es el conjunto formado por todos los valores que puede llegar a tomar la función

Rango:

En estadistica descriptiva se denomina rango estadístico (R) o recorrido estadístico al intervalo a la diferencia entre el valor máximo y el valor mínimo; por ello, comparte unidades con los datos. Permite obtener una idea de la dispersión de los datos, cuanto mayor es el rango, más dispersos están los datos de un conjunto.

Por ejemplo, para una serie de datos de carácter cuantitativo, como lo es la estatura medida en centímetros, tendríamos:

es posible ordenar los datos como sigue:

donde la notación x_(i) indica que se trata del elemento i-ésimo de la serie de datos. De este modo, el rango sería la diferencia entre el valor máximo (k) y el mínimo; o, lo que es lo mismo:

En nuestro ejemplo, con cinco valores, nos da que R = 185-155 = 30.

Variable:

 El término «variable» se utiliza aún fuera del ámbito matemático para designar una cantidad susceptible de tomar distintos valores numéricos dentro de un conjunto de números especificado.¹

Constante:

Una constante es un valor que no cambia (aunque puede no ser conocido, o indeterminado). En este contexto, debe diferenciarse de una constante matematica, que es una magnitud numérica específica, independientemente de la naturaleza del problema dado.